Monthly Archives: June 2017

by ksackel | June 30, 2017 · 2:54 pm

Kylerec – On J-holomorphic curves, part 2

This is a continuation post following part 1. Hope the delay wasn’t too long – more coming soon.

A preparatory comment on last time

Let us quickly recall the proof sketched in part 1 that fillable implies tight for contact $(M^3,\xi)$ . The idea was that if we had a filling $W$ , then the presence of an overtwisted disk locally gave a Bishop family of holomorphic disks as part of a 1-dimensional moduli space, but the compactified moduli space was seen to have only one boundary point. This was because continuing the family away from the center of the overtwisted disk could not lead to a possible boundary point – in our version, such a point would require a bubble, but we considered exact fillings.

It was mentioned last time that Eliashberg’s paper on fillings by holomorphic disks actually covers the weak case instead. The difference is that one now instead shows that any closed surface in a contact boundary which is weakly filled indeed bounds a 3-manifold which can be foliated by holomorphic disks. With this result, we never actually need to consider bubbles on the interior, so we can remove the exactness assumption.

I want to point this out because although this isn’t perfectly analagous to the discussion in the next section on Wendl’s paper, it is related in basic idea. The set-up is different, sure, and also one cannot work directly with the contact manifold with its filling (the necessity of a strong filling appears in the need to attach a positive cylindrical end), and finally also the completed foliation does have (isolated) nodal curves, but in the end we end up with a nice Lefschetz fibration with holomorphic fibers, and that’s pretty powerful, just like Eliashberg’s disk fillings. We explain this… now!

On Wendl’s Strongly fillable contact manifolds and J-holomorphic foliations

I should say, first of all, that one can generalize the results I am discussing here. For a somewhat more general discussion, see this post by Laura Starkston from 2013.

In this section, all contact manifolds are 3-dimensional and all symplectic manifolds are 4-dimensional.

We begin by recalling that the symplectization of a cooriented contact manifold $(M,\xi = \ker \alpha)$ is the symplectic manifold $(\mathbb{R} \times M, d(e^t\alpha))$ , where $t$ is the $\mathbb{R}$ -coordinate. This symplectic manifold does not depend upon the choice of $\alpha$ , since if we chose $\alpha' = e^f \alpha$ , then $d(e^t\alpha') = d(e^{t+f}\alpha) = \phi^* d(e^t\alpha)$ where $\phi$ is the diffeomorphism of $\mathbb{R} \times M$ sending $(t,m) \mapsto (t+f(m),m)$ .

Remark: One can define this in a more invariant way. The symplectization of $(M,\xi)$ is the set of covectors vanishing on $\xi$ . This is an $\mathbb{R}^*$ -bundle over $M$ and is symplectic with respect to the standard symplectic form on $T^*M$ . Fixing a local section $\alpha$ over $M$ gives a coordinate $w$ for the fiber such that the symplectic form is just $d(w\alpha)$ . We simply take the component where $e^t := w > 0$ and $\alpha$ coorients $\xi$ .

Given a symplectization, explicitly determined by a chosen contact form $\alpha$ , one typically studies J-holomorphic curves only for choices of $J$ which are admissible, meaning:

$J$ is $\mathbb{R}$ -invariant
$J \partial_t = R_{\alpha}$
$J|_{\xi}$ is a compatible almost complex structure for $d\alpha|_{\xi}$

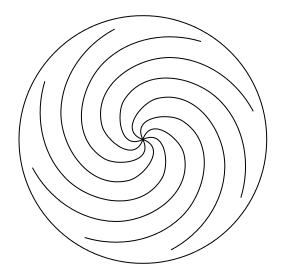
Under these conditions, finite energy J-holomorphic curves from punctured Riemann surfaces are analytically easy to understand – the punctures are asymptotic to Reeb orbits at the positive and negative ends, and Gromov compactness extends to this setting in that one needs to include holomorphic buildings. One can imagine, for example a sequence of $J$ -holomorphic curves which look like some union of cylinders over Reeb orbits for all but a union of two intervals $(-A-C,-A) \cup (A,A+C)$ on which there is nontrivial behavior, where $C$ remains fixed but $A \rightarrow \infty$ . In the limit, as these two intervals get farther apart, we break into two holomorphic curves in the symplectization. This forms what is sometimes called a holomorphic building. In general, there may be multiple levels in the limit, as in the figure below.

Here, a J-holomorphic curve gets stretched out in two places, shown in green, until eventually these green almost cylindrical parts get infinitely long. In the limit, we obtain a three story holomorphic building.

For more details in much more generality, one should consult this paper of Bourgeois, Eliashberg, Hofer, Wysocki, and Zehnder.

Now suppose that we have a strong filling $(W,\omega)$ of a contact manifold $(M,\xi)$ . Then by definition, we have a Liouville vector field $V$ whose flow allows me to identify a neighborhood of $M$ with a subset of the symplectization of the form $((-\epsilon,0] \times M, d(e^t\alpha))$ where $\alpha$ is a contact form for $\xi$ on $M$ . One can append the rest of the positive end of the symplectization, $([0,\infty) \times M, d(e^t\alpha))$ , to form a completed symplectic manifold $(\widehat{W},\widehat{\omega})$ . I can choose some compatible almost complex structure $J$ which far enough into the positive end is a restriction of some admissible $J_+$ . In this case, one can study J-holomorphic curves, and we have a similar Gromov compactness statement. In this case, our curves can either bubble, or form holomorphic buildings where the lowest level is just $(\widehat{W},J)$ and whose higher levels are all $(\mathbb{R} \times M, J_+)$ .

Theorem (vaguely stated): Under some technical analytical conditions, an $\mathbb{R}$ -invariant foliation of $\mathbb{R} \times M$ by $J$ -holomorphic curves of uniformly bounded energy will extend, with isolated nodal singularities, to the interior of $W$ (and hence to all of $\widehat{W}$ ).

Proof (sketch): We study the compactification of the moduli space $\mathcal{M}$ of finite energy J-holomorphic curves in $\widehat{W}$ , and in particular, the closure of the component $\mathcal{M}_0$ of the moduli space containing a special leaf in the symplectization end. This component is 2-dimensional, and hence is precisely given by the foliating leaves around it (recall $\widehat{W}$ is 4-dimensional). The closure of this component yields the full J-holomorphic foliation, where some isolated finite subset of the leaves are actually nodal curves.

In the end, by considering on which curve in the foliation a point is located, this yields a map $\pi \colon \widehat{W} \rightarrow \overline{\mathcal{M}_0}$ , where the fibers are symplectic (since they are J-holomorphic and $J$ is compatible with $\widehat{\omega}$ ) and generically smooth except with finitely many nodal singular fibers, forming what is called a symplectic Lefschetz fibration.

We will discuss this notion more in a future post, where we will also see that Stein fillings correspond in some sense to certain (“allowable”) symplectic Lefschetz fibrations over a disk. Hence, one can ask – are there some examples of contact manfiolds $(M,\xi)$ on which we can find a finite energy foliation on the symplectization $\mathbb{R} \times M$ satisfying the correct analytical assumptions and such that $\overline{\mathcal{M}_0} = \mathbb{D}$ ? The answer is yes in the case when $(M,\xi)$ is supported by a so-called planar open book, as was proved in this paper by Wendl. We will define this in a future post, but this discussion implies (up to how to tackle the word “allowable”) that:

Corollary: For contact 3-manifolds supported by a planar open book, strong and Stein fillability are equivalent.

Along similar lines, one can find finite energy foliations for the standard 3-torus $(\mathbb{T}^3,\xi_0)$ (with contact structure induced by the restriction of the Liouville form on $T^*\mathbb{T}^2$ to the unit cotangent bundle). In this case, any strong filling, not just the standard one, would have $\overline{\mathcal{M}_0} = [0,1] \times S^1$ , and so any strong filling of $(\mathbb{T}^3,\xi_0)$ arises as the boundary of a Lefschetz fibration to $[0,1] \times S^1$ . Wendl then beefs this up to prove, for example, that every minimal strong filling of $(\mathbb{T}^3,\xi_0)$ is diffeomorphic to $\mathbb{T}^2 \times \mathbb{D}$ .

Finally, one can use these results to obstruct strong fillability in a manner analogous to the Bishop family argument. That is, if $(M,\xi)$ has a finite energy foliation satisfying the technical analytic assumptions, then one should be able to extend that foliation to a strong filling. Recall that the foliation extended by considering the component of the moduli space containing some specified leaf $u_0$ satisfying some conditions. If there is some other leaf $u_1$ which is not diffeomorphic to $u_0$ , then they cannot both be fibers of the same Lefschetz fibration, and so there couldn’t have been a strong filling in the first place. There are also other more technical versions of this argument, which for example allow one to reprove that positive Giroux torsion, i.e. that there is a contact embedding of $([0,1] \times T^2, \cos(2\pi t)d\theta_1 + \sin(2\pi t)d\theta_2)$ , obstructs fillability, originally proved by David Gay using gauge-theoretic methods which are completely avoided in this approach.

On Barth-Geiges-Zehmisch’ The diffeomorphism type of fillings

As we have now seen twice, the technique of comparing moduli spaces of J-holomorphic curves to the topology of the situation in question is very powerful. We saw this both in our discussion last time of McDuff’s rational ruled classification, and we also just saw in our discussion of Wendl’s paper that the breaking which occurs in the compactification of a certain moduli space of curves in a strong filling of the positive end of a symplectization actually cooks up a Lefschetz fibration. One can view this paper as another instance of this way of thinking – here evaluation maps end up directly producing strong restrictions on the topology of a filling.

As we will see in a future post, Weinstein fillings of contact manifolds $(M^{2n+1},\xi)$ have a surgery theory consisting of handles of index at most $n$ , and so they have the homotopy type of a CW complex of at most this dimension. A subcritical Weinstein filling is then one where all the handles have index at most $n-1$ . The main theorem states that the existence of just one subcritical Weinstein filling places restrictions on the topology of any strong symplectically aspherical filling $(W,\omega)$ . By symplectically aspherical, we mean that $\omega|_{\pi_2(W)} = 0$ .

Theorem [BGZ]: If $(M,\xi)$ is a contact manifold of dimension $\geq 3$ admitting a subcritical Stein filling with the homotopy type of a CW complex of dimension $\ell_0$ , then any strong symplectically aspherical filling $(W,\omega)$ satisfies

$H_k(W) = H_k(M)$ for $k = 0,\ldots, \ell_0$ via the isomorphism induced by inclusion
$H_k(W) = 0$ otherwise
If $\pi_1(M) = 0$ , then all strong aspherical fillings of $M$ are diffeomorphic.

Corollary [Eliashberg-Floer-McDuff ’91]: Every symplectically aspherical filling of the standard contact sphere is diffeomorphic to a ball.

Remark: For $S^3$ , which is just the lens space $L(1,1)$ , McDuff’s theorem from last time about fillings of lens spaces implies that there is a unique minimal filling up to diffeomorphism. By positivity of intersection, symplectically aspherical fillings are minimal, which implies the above result. But also, since $\omega$ is automatically a trivial cohomology class on the ball, McDuff’s result implies that the filling is in fact unique up to symplectomorphism. This result goes back to Gromov’s ’85 paper.

We won’t quite make it to a proof of the full theorem, but we will see some of the inner workings in the statement of the theorem stated below. We proceed by making an extra definition (not in Barth-Geiges-Zehmisch) to clarify the exposition.

Definition: Let $(M^{2n+1},\xi)$ be a connected contact manifold and $(V^{2n},\omega = d\lambda)$ a Liouville manifold of finite type (meaning it is modelled after a positive symplectization outside of some compact region). Let $\mathcal{L}$ be the corresponding Liouville vector field (satisfying $i_{\mathcal{L}}\omega = \lambda$ ). The $M$ is called $V$ –spliffable (yes, this is what we called it at Kylerec) if $M$ is contactomorphic to a hypersurface $\widetilde{M}$ in $V \times \mathbb{C}$ such that:

$\widetilde{M}$ is convex, meaning it is transverse to the vector field $\mathcal{L} \oplus \partial_r$ where $\partial_r$ is the standard radial Liouville vector field on $\mathbb{C}$
the infinite component of $V \times \mathbb{C} \setminus \widetilde{M}$ is modelled after the positive symplectization of $M$ meaning this component is the union of the positive flow of $\widetilde{M}$ along $\mathcal{L} \oplus \partial_r$

Remark: A contact manifold which is fillable by a subcritical Weinstein manifold is spliffable. This follows from a result of Cieliebak that subcritical Stein manifolds are split.

Theorem: Let $(W,\omega)$ be an aspherical strong filling of a $V$ -spliffable contact manifold $M$ . Then there exists a commutative diagram of the form

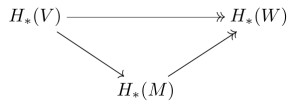
BGZ_Diagram_Theorem

(and similarly with $H_*$ replaced with $\pi_1$ ).

Remark: The Eliashberg-Floer-McDuff theorem is already a corollary of this weaker statement, using that $S^{2n-1}$ is $\mathbb{C}^{n-1}$ -spliffable, and using smooth topology.

Corollary: The unit cotangent bundle $M = S^*\Sigma$ of a closed manifold $\Sigma^n$ admits no subcritical Weinstein fillings.

Proof: We need $H_n(V)$ surjects onto $H_n(W) \neq 0$ with $W$ the standard unit disk filling and $M$ is $V$ -spliffable. But if $M$ admits a subcritical filling, then $V$ can be chosen to be subcritical so that $H_n(V) = 0$ . This is a contradiction.

Proof of the main theorem:

We begin by embedding $M$ into $V \times \mathbb{D}$ so that it is convex (which we can do by the spliffability condition). The interior component determine by the splitting through $M$ can then be replaced by $W$ by gluing in (since strong gluings are set up to be Liouville near the boundary). Call the interior of this manifold $Z$ . We can then choose a map $\mathbb{D} \rightarrow \mathbb{C}P^1$ such that the interior embeds diffeomorphically onto $\mathbb{C}P^1 \setminus \{\infty\}$ . This embedding then gives us a smooth manifold $\widetilde{Z}$ which looks like $V \times \mathbb{C}P^1$ but with the interior component replaced by $W$ . That is, $\widetilde{Z} = Z \cup (V \times \{\infty\})$ .

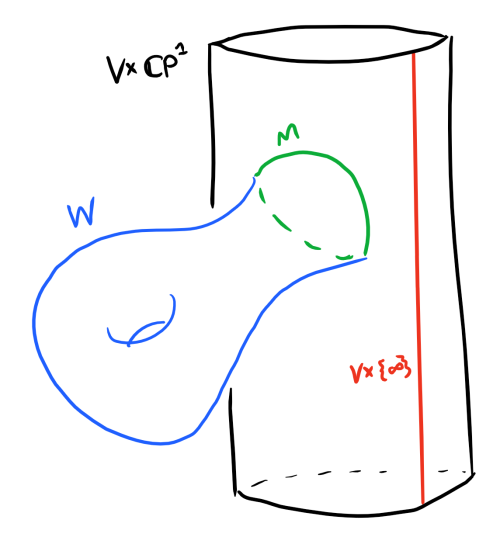
BGZ_Setup

We then wish to study some $J$ -holomorphic curves on this manifold. We pick a compatible $J$ which away from $W$ is of the form $J_V \oplus i_{\text{std}}$ , where $J_V$ is admissible (as discussed in the previous section) for $V$ . We study the moduli space $\mathcal{M}$ of $J$ -holomorphic spheres $u \colon \mathbb{C}P^1 \rightarrow \widetilde{Z}$ such that $[u] = [\{v\} \times \mathbb{C}P^1]$ (for some $v$ large enough so that this slice misses $W$ ). We really want this up to reparametrization, so we fix slice conditions to define this moduli space: that $u(-1) \in V\times \{a\}$ , $u(+1) \in V \times \{b\}$ , and $u(\infty) \in V \times \{\infty\}$ , for some choice of $a,b \in \mathbb{C}P^1$ distinct and not $\infty$ .

The key about positive symplectization ends is that admissibility of the almost complex structure $J$ implies a maximum principle for these curves. This implies the following two items.

Since $V \times \mathbb{C}P^1$ looks like a symplectization, in $\widetilde{Z}$ , any curve in our moduli space must have actually just been $\{v\} \times \mathbb{C}P^1$ .
Any curve in our moduli space intersecting $W$ must intersect $V \times \{\infty\}$ . First of all, $W$ is symplectically aspherical, so any holomorphic sphere must leave $W$ . But then, if it didn’t intersect $V \times \{\infty\}$ , it would be contained completely in $V \times \mathbb{C}$ , which contradicts this maximum principle.

Now, this moduli space is an oriented manifold of dimension $2n$ , and it comes with an evaluation map of the form $\mathcal{M} \times \mathbb{C}P^1 \rightarrow \widetilde{Z}$ . This map is actually proper and degree 1, which follows from the maximum principles just described, plus a little boost from positivity of intersection which implies that there is no need to worry about stable maps in the compactification of $\mathcal{M}$ . This then restricts to a proper degree 1 evaluation map $\mathcal{M} \times \mathbb{C} \rightarrow Z$ .

Hence, we obtain the following commutative diagram.

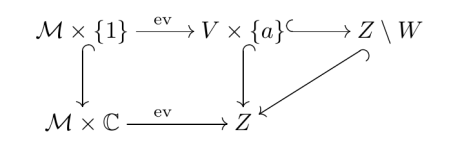
BGZ_Diagram_Proof

In homology, the right triangle becomes the desired triangle from the theorem.

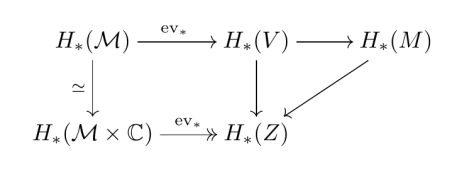
BGZ_Diagram_Proof_2

As for the surjectivity part of the theorem, note that the leftmost vertical arrow is an isomorphism. Meanwhile, the bottom horizontal arrow is surjective for standard topological reasons (because one can cook up an explicit shriek map $\text{ev}_!$ which is right inverse to $\text{ev}_*$ on the level of homology).

2 Comments

Filed under Uncategorized

by ksackel | June 14, 2017 · 1:36 pm

Kylerec – On J-holomorphic curves, part 1

This to-be-2-part-because-this-got-long post is a continuation of the series on Kylerec 2017 starting with the previous post, and covers most of the talks from Days 2-3 of Kylerec, focusing on the use of J-holomorphic curves in the study of fillings. I should mention that two more sets of notes, by Orsola Capovilla-Searle and Cédric de Groote, have been uploaded to the website on this page. So if you wish to follow along, feel free to follow the notes there, and in particular, the relevant talks I’ll be discussing in this post are:

Part 1

Day 1 Talk 1 – The introductory talk by (mostly) Roger Casals (with some words by Laura Starkston)
Day 2 Talk 2 – Roberta Gaudagni’s talk introducing J-holomorphic curves
Day 2 Talk 3 – Emily Maw’s talk on McDuff’s rational ruled classification

Part 2

Day 2 Talk 4 – Agustín Moreno’s talk on Wendl’s J-holomorphic foliations
Day 3 Talk 1 – Umut Varolgüneş’ talk on Barth-Geiges-Zehmisch’ diffeomorphism types of symplectic fillings

It should be obvious in what follows which parts of the exposition correspond to which talks, although what follows is perhaps a pretty biased account, with some parts amplified or added, and others skimmed or skipped.

J-holomorphic curves – basics

Gromov introduced the study of J-holomorphic curves into symplectic geometry in his famous 1985 paper, immediately revolutionizing the field. One might wonder why we care about these objects, and the rest of this post (along with part 2) should be a testament to some (but certainly not all) aspects of the power of the theory.

The “J” in “J-holomorphic” refers to some choice $J$ of almost complex structure on a manifold $M^{2n}$ . Given an almost complex manifold, a J-holomorphic curve is a map $u : (\Sigma,j) \rightarrow (M^{2n},J)$ such that $(\Sigma,j)$ is a Riemann surface and $J \circ du = du \circ j$ . In the case where $(M,J)$ is a complex manifold, we see this is precisely what it means to be holomorphic.

We are mostly concerned a choice of $J$ which is compatible with a symplectic manifold $(M,\omega)$ . By this, we mean that the (0,2)-tensor $g(\cdot, \cdot) = \omega(\cdot,J\cdot)$ is a Riemannian metric. We say $J$ is tame if $\omega(v,Jv) > 0$ for each nonzero vector $v$ (note that $g$ as defined above is not necessarily symmetric in this case).

Proposition: The space of compatible almost complex structures on a symplectic manifold $(M,\omega)$ is non-empty and contractible. So is the space of tame almost complex structures.

This suggests either:

Studying the space of J-holomorphic curves into $M$ for some particular choice of $J$ .
Study some invariant of spaces of J-holomorphic curves which does not depend on the choice of $J$ compatible (or tame) with respect to a given symplectic form $(M,\omega)$ .

In walking down either of these paths, there are a large number of properties at our disposal. What is presented in this section is far from a conclusive list, and I have completely abandoned including proofs and motivation, so beware that there is a lot of subtlety involved in the analytic details. For many many many more details, consult this book of McDuff and Salamon.

Firstly, there is a dichotomy between somewhere injective curves and multiple covers. Some J-holomorphic curves will factor through branched covers, meaning that $u : \Sigma \rightarrow (M,J)$ factors as $(\Sigma,j) \rightarrow (\Sigma',j') \rightarrow (M,J)$ such that the first map is a branched cover of Riemann surfaces. J-holomorphic curves which are not multiply covered are called simple, and it turns out that simple curves are characterized by being somewhere injective, meaning there is some $z$ for which $u^{-1}u(z) = \{z\}$ and $du_z \neq 0$ . Even better, somewhere injective means that $u$ is almost everywhere injective.

The main tool in the theory is the study of certain moduli spaces of J-holomorphic curves. There are many flavors of this, but we discuss a specific example to highlight the relevant aspects of the theory. The analytical details are typically easier for simple curves, so we denote by $\mathcal{M}^*(M,J)$ the moduli space of all simple $J$ -holomorphic curves. It turns out to be fruitful to focus in on a specific piece of this space, so we often restrict to a given domain of definition, say some $\Sigma_g$ , and also restrict the homology class $u_*[\Sigma]$ of the map $u : \Sigma_g \rightarrow (M,J)$ to some $A \in H_2(M)$ . The main question is:

When is such a moduli space $\mathcal{M}_g^*(M,A,J)$ actually a smooth manifold?

This is certainly a subtle question, and it turns out that not every $J$ works. However, it is a theorem that for generic $J$ , this moduli space is a smooth manifold of dimension $d = n(2-2g) + 2c_1(A)$ , where $\dim M = 2n$ .

Given our nice moduli space, we also might be interested in what happens as we change our choice of $J$ , so that we go from one regular choice to another. A generic path of such almost complex structures will give a smooth cobordism between the moduli spaces, a property which allows us to cook up invariants which do not depend, for example, on choices of $J$ compatible with a given symplectic structure.

To note a few variants of the discussion so far, sometimes we will study J-holomorphic disks with certain boundary conditions, or J-holomorphic curves with punctures sent to a certain asymptotic limit. In all cases, the same analytic machinery already swept under the rug (Fredholm theory) will give that the moduli spaces in question are smooth for generic choices of almost complex structure, and the dimension of this moduli space is given by some purely topological quantity (by, for example, the Atiyah-Singer index theorem).

One common thing to do is to quotient out by the group action given by reparametrizing the domain of a given J-holomorphic curve. That is, we consider the equivalence relation $u \sim u \circ \phi$ where $\phi : (\Sigma,j) \rightarrow (\Sigma,j)$ is a biholomorphism. A more careful author would probably distinguish between the map $u$ as opposed to the corresponding equivalence class, which is really what one should mean when they say curve. Hence, one can quotient our moduli spaces $\mathcal{M}^*$ by reparametrization to obtain moduli spaces of curves. Usually, these are the main objects of interest.

So now we have our nice moduli space, in whatever situation we desire, and we can ask about studying limits of J-holomorphic curves in that moduli space. In general, no such curve might exist. The first reason for this is that any such curve $u : (\Sigma,j) \rightarrow (M,\omega,J)$ has an energy $E = \int_{\Sigma}u^*\omega$ attached to it (when $J$ is compatible with $\omega$ ). If this quantity diverges to $\infty$ , then there can be no limiting curve. One can ask instead about what happens when the energy is bounded.

Consider the following sequence of holomorphic curves $u_n \colon \mathbb{C}P^1 \rightarrow \mathbb{C}P^1 \times \mathbb{C}P^1$ given by $z \mapsto (z, 1/(nz))$ . We see that away from $z=0$ , this is just converging to the curve $\mathbb{C}P^1 \times \{0\}$ . But near $z = 0$ , if we reparametrize the domain by $1/(nz)$ , we see this converges to the sphere $\{0\} \times \mathbb{C}P^1$ . In this case, our curve formed what is often called a bubble. More generally, a curve can split off many bubbles at a time. For an example of this, consider instead $u_n \colon \mathbb{C}P^1 \rightarrow \mathbb{C}P^1 \times \mathbb{C}P^1 \times \mathbb{C}P^1$ given by $z \mapsto (z,1/(nz),1/(n^2z))$ , in which a new bubble forms at $\{0\} \times \{\infty\} \times \mathbb{C}P^1$ in addition to the one discussed above. More generally, a sequence of curves can limit to a curve with trees of bubbles sticking out.

Stable_Curve

Such bubble trees are called stable or nodal or cusp curves (or probably a lot of other things), depending upon how old your reference is and to whom you talk. The incredible theorem, which goes under the name of Gromov compactness, is that this is the only phenomenon which precludes a limit from existing. We state this vaguely as follows:

Theorem [Gromov ’85]: The moduli space of curves of energy bounded by some constant $E$ (modulo reparametrization of domain) can be compactified by adding in stable curves of total energy bounded by $E$ .

Another generally important tool is that of the evaluation map. Suppose that we wish to study the moduli space $\mathcal{M}_g^*(M,A,J)$ of simple J-holomorphic maps $u : (\Sigma_g,j) \rightarrow (M,J)$ in the homology class $A \in H_2(M)$ . Suppose $G = \text{Aut}(\Sigma_g,j)$ is the group of biholomorphisms of $(\Sigma_g,j)$ . Then the group $G$ acts on $\mathcal{M}_g^*(M,A,J) \times \Sigma_g$ by $\phi \cdot (u,z) = (u \circ \phi^{-1},\phi(z))$ . Notice then that the evaluation map $(u,z) \mapsto u(z)$ only depends on the orbit, and hence descends to a map $\text{ev} : \mathcal{M}_g^*(M,A,J) \times_G \Sigma_g \rightarrow M$ . Proving enough properties of such an evaluation map sometimes allows us to compare the smooth topology of $\mathcal{M}_g^*(M,A,J)$ to that of $M$ . There are other variants of this – sometimes we wish to evaluate at multiple points, or sometimes we consider J-holomorphic discs and want to evaluate along boundary points. And often the evaluation map extends to the compactified moduli spaces considered above.

Finally, we come to dimension 4, where curves might actually generically intersect each other. With respect to these intersections, there are two key results to highlight. The first is positivity of intersection (due to Gromov and McDuff), which states that if any two J-holomorphic curves intersect, then the algebraic intersection number at each intersection point is positive (and precisely equal to 1 at transverse intersections). This can be thought of as some sort of rudimentary version of a so-called adjunction inequality (due to McDuff), which states that if $u \colon (\Sigma,j) \rightarrow (M,J)$ is a simple J-holomorphic curve representing the class $A$ with geometric self-intersection number $\delta(u)$ , then

$c_1(TV,J) \cdot A + 2\delta(u) \leq \chi(\Sigma) + A \cdot A$ .

Further, when $u$ is immersed and with transverse self-intersections, this is an equality, yielding an adjunction formula.

A first example – Fillable implies tight (in 3 dimensions)

On a first pass, I want to expand upon the example of fillability implying tightness in three dimensions which Roger Casals discussed in his introductory talk. Really, we prove the contrapositive – that an overtwisted contact manifold cannot be filled. For simplicity, we will consider exact fillings. This result is typically attributed to Gromov and Eliashberg, referencing Gromov’s ’85 paper as well as Eliashberg’s paper on filling by holomorphic discs from ’89. This is essentially the same proof in spirit, although we take a little bit of a cheat by considering exact fillings.

Firstly, recall that an overtwisted contact manifold $(M^3,\xi)$ is one such that there exists an embedding of a disk $\phi : D^2 \hookrightarrow M$ , such that the so-called characteristic foliation $(d\phi)^{-1}\xi$ on $D^2$ , which is actually a singular foliation, looks like the following image, with one singular point in the center and a closed leaf as boundary.

OT_Disk

So now suppose $(M^3,\xi)$ has an exact filling $(W^4,\omega = d\lambda)$ . We study the space of certain J-holomorphic disks with boundary on the overtwisted disk. The key is that a neighborhood of the overtwisted disk $D$ actually has a canonical neighborhood in $W$ up to symplectomorphism, and one can pick an almost complex structure $J$ to be in a standard form in this neighborhood. It turns out that with this standard choice, in a close enough neighborhood of the singular point $p$ in the interior of $D$ , all somewhere injective J-holomorphic curves are precisely those living in a 1-parameter family, called the Bishop family, which radiate outwards from the singular point $p$ .

Let us be a bit more precise, so that we can see this Bishop family explictly. Consider the standard 3-sphere $S^3 \subset \mathbb{C}^2$ , with its standard contact structure given by the complex tangencies, i.e. $\xi = TS^3 \cap iTS^3$ , with $i$ the standard complex structure on $\mathbb{C}^2$ . Then consider the disk given by $z \mapsto (z, \sqrt{1-|z|^2})$ . The characteristic foliation on this disk looks like the characteristic foliation near the center of the overtwisted disk, so a neighborhood of this disk in $D^4 \subset \mathbb{C}^2$ yields a model for a neighborhood of the center of the overtwisted disk. We may assume the almost complex structure in this neighborhood is just given by the standard one, $i$ . Then the Bishop family is just the sequence of holomorphic disks given by $z \mapsto (sz,\sqrt{1-s^2})$ for $s$ a real constant near 0. That these are all of the somewhere injective disks is a relatively easy exercise in analysis. Namely, suppose we had such a disk of the form $z \mapsto (v_1(z),v_2(z))$ . Then since boundary points are mapped to the overtwisted disk, $v_2(\partial D^2) \subset \mathbb{R}$ . But each component of $v_2$ is harmonic, hence satisfies a maximum principle. Therefore, $v_2(D^2) \subset \mathbb{R}$ . But by holomorphicity, $v_2$ cannot have real rank 1 and so must be constant. Hence, any disk in consideration must have $v_2$ is a real constant.

All of these disks live in $D^4 \subset \mathbb{C}^2$ , but in particular in the slice where the second component $z_2$ is real, so we can draw this situation in $\mathbb{R}^3$ by forgetting the imaginary part of $z_2$ . This is depicted in the following figure.

Bishop_Family

This Bishop family lives in some component of the moduli space of somewhere injective J-holomorphic disks with boundary on $D$ . Perturbing $J$ , one can assume this component is actually a smooth 1-dimensional manifold. We can compactify this moduli space by including stable maps, i.e. disks with bubbles, via Gromov compactness. On the Bishop family end, we see explicitly that the limit is just the constant disk at the point $p$ . So there must be another stable curve at the other boundary of this moduli space. We prove no such other stable curve can exist.

Similar to how we proved that the only disks completely contained in a neighborhood of the singular point on the overtwisted disk must have been part of the Bishop family, one can use a maximum principle argument to conclude that every holomorphic disk entering this neighborhood must have been in the Bishop family. Alternatively, one can use a modified version of positivity of intersections to conclude that continuing the moduli space away from the Bishop family, these boundaries have to continue radiating outward. Either way, the moduli space has to stay away from the central singularity of the overtwisted disk $D$ . But also, the boundary of a J-holomorphic disk cannot be tangent to $\xi$ , and in particular cannot be tangent to $\partial D$ . This is by a maximum principle which comes from analytic convexity properties of a filled contact manifold.

The only possible explanation is that this is a stable curve with some sphere bubble having formed in the interior of $(W,\lambda)$ . But one checks that the relation $g(\cdot,\cdot) = \omega(\cdot,J\cdot)$ implies that for a $J$ -holomorphic sphere $u : (S^2,j) \rightarrow (W,J)$ , we have $\text{Area}_g(u) = \int_{S^2}u^*\omega$ . This vanishes by Stokes’ Theorem since $\omega = d\lambda$ is exact, and so $u$ must be constant, and so there is no bubble. In other words, this cannot explain the other boundary point of the component of the moduli space containing the Bishop family, so this yields a contradiction.

On McDuff’s The structure of ruled and rational symplectic 4-manifolds

Emily Maw’s talk from the workshop followed this paper by Dusa McDuff. In what follows, we shall consider triples $(V,C,\omega)$ such that $(V,\omega)$ is a smooth closed symplectic 4-manifold and $C$ is a rational curve, by which we mean a symplectically embedded $S^2$ . We call a rational curve $C$ exceptional if $C \cdot C = -1$ with respect to the intersection product on $H_2(V)$ (with respect to its orientation coming from $\omega$ ). We say $(V,C,\omega)$ is minimal if $V \setminus C$ contains no exceptional curves. The main theorem is as follows:

Theorem [McDuff ’90]: If $(V,C,\omega)$ is minimal and $C \cdot C \geq 0$ , then $(V,\omega)$ is symplectomorphic to either:

$(\mathbb{C} P^2, \omega_{FS})$ , in which case $C$ is either a complex line or a quadric (up to symplectomorphism).
A symplectic $S^2$ -bundle over a compact manifold $M$ , in which case $C$ is either a fiber or a section (up to symplectomorphism).

Before describing the proof, which is the part involving J-holomorphic curve techniques, we apply this to strong fillings. We shall concern ourselves with fillings of the lens spaces $L(p,1)$ with their standard contact structures, where $p > 0$ is an integer. Let us first define this contact structure. Recall that the standard contact structure on $S^3$ is the one coming from complex tangencies by viewing $S^3 \subset \mathbb{C}^2$ . Then the standard contact structure on $L(p,1)$ is the one given by the quotient $L(p,1) = S^3/(\mathbb{Z}/p\mathbb{Z})$ where the action of $1 \in \mathbb{Z}/p\mathbb{Z}$ given by $(z_1,z_2) \mapsto e^{2\pi i/p}(z_1,z_2)$ preserves the contact structure, so that it descends.

Theorem [McDuff ’90]: The lens spaces $L(p,1)$ all have minimal symplectic fillings $(Z,\omega)$ , and when $p \neq 4$ , these fillings are unique up to diffeomorphism, and further up to symplectomorphism upon fixing the cohomology class $[\omega]$ . The space $L(4,1)$ has two nondiffeomorphic minimal fillings.

Proof (sketch): The complex line bundle $\mathcal{O}(p)$ over $S^2$ comes with a natural symplectic structure, and this forms a cap for $L(p,1)$ . The zero section of $\mathcal{O}(p)$ is a rational curve of self intersection $p > 0$ . McDuff’s explicit classification includes examples $(V,C)$ for any such given $p$ , and $V \setminus C$ thus gives a minimal filling for $L(p,1)$ . The remaining statements come from a more detailed analysis of the classification result.

Now, I will not go through all of the details of McDuff’s proof of the main theorem, but I will highlight where various J-holomorphic tools appear in the proof. Let me break up the proof into two big pieces.

Step 1: “Mega-Lemma” Consider $(V,C,\omega)$ minimal as above. There is a tame almost complex structure $J$ such that $[C]$ can be represented by a $J$ -holomorphic stable curve of the form $S = S_1 \cup \cdots \cup S_m$ , where:

Each $A_i := [S_i]$ is $J$ -indecomposable (meaning any stable curve representing $A_i$ must actually be a legitimate curve of one component)
The almost complex structure $J$ is regular for all curves in the class $A_i$ .
The $S_i$ are distinct and embedded curves of self-intersection -1, 0, or 1, with at least one index for which $A_i \cdot A_i \geq 0$ .

We didn’t prove this at the workshop, so I won’t discuss it in detail here. But this is a major reduction into cases. For example, if $m = 1$ and $S \cdot S = 1$ , then it had already been shown that this implies that $V = \mathbb{C}P^2$ . This bleeds into…

Step 2: Using the evaluation maps constructively

Let us discuss the proof of this last fact briefly. The idea is as follows. We consider the moduli space $\mathcal{M}^*(A,J)$ consisting of simple holomorphic spheres representing the class $A = [S]$ . This comes with an evaluation map of the form

$\mathcal{M}^*(A,J) \times_{G} (S^2 \times S^2) \rightarrow V \times V$

where $G$ is the group of automorphisms of $S^2$ . Both sides have dimension 8 and this evaluation map is injective away from the diagonal since $A \cdot A = 1$ and we have positivity of intersection. Therefore, this map has degree 1, and so any pair of distinct points on $V$ has a unique curve passing through it. This is enough to show $V = \mathbb{C}P^2$ .

Let us do another case, but show that the adjunction formula also comes into play.

Proposition: Suppose $B$ is a simple homology class in $(V,\omega)$ (i.e. is not a multiple of another homology class) with $B \cdot B = 0$ , and suppose $F$ is a rational embedded sphere representing $B$ . Then there is a fibration $\pi \colon V \rightarrow M$ with symplectic fibers and such that $F$ is one of the fibers.

Proof (sketch): The idea is to consider the moduli space $\mathcal{M}^*_{0,1}(V,J,B)$ of rational embedded $J$ -holomorphic curves with 1 marked point $p \in S^2$ , and where $J$ is chosen to tame $\omega$ and such that $F$ is itself a $J$ -holomorphic curve, and where we have quotiented by reparametrization of the domain. Then one can compute the dimension of this moduli space at a given curve $C$ in the appropriate way as

$d = \dim V + 2c_1(TV) \cdot [C] - 4$ ,

where the last -4 comes from quotienting by the subgroup of $PSL_2(\mathbb{C})$ fixing the marked point. Applying adjunction for the curve represented by $F$ , so that $[C] \cdot [C] = 0$ , yields $d = 4$ . We also have an evaluation map

$\text{ev} : \mathcal{M}^*_{0,1}(V,J,B) \rightarrow V$

Since $B \cdot B = 0$ , there is at most one $B$ -curve through each point in $V$ , so it follows that this evaluation map has degree at most 1, and hence equal to 1 by regularity. This yields the structure of a fibration $\pi : V \rightarrow M$ where the fibers are precisely the curves in our moduli space. Since the fibers are holomorphic, they are symplectic by the taming condition.

2 Comments

Filed under Uncategorized

by ksackel | June 2, 2017 · 9:54 am

Kylerec Overview

Updates (June 11, 2017): Added link to other notes from Kylerec workshop, and fixed an error caught by Chris Wendl in the comments.

I’m very excited to be joining this blog!

This is the first of a series of posts about the content of the Kylerec workshop, held May 19-25 near Lake Tahoe, which focused on fillings of contact manifolds. Under the guidance of our mentors, Roger Casals, Steven Sivek, and Laura Starkston, we worked from the basic theory of fillings through some state-of-the-art results. Many of the basics have been discussed on this blog already in Laura Starkston’s posts from January 2013: Part 1 and Part 2 on Fillings of Contact Manifolds. For a more thorough introduction to types of filling and the differences between them, I suggest reading those posts (and the accompanying comments by Paolo Ghiginni and Chris Wendl). This post will remain self-contained anyway.

One can find notes that I took (except for three lectures, due to technical difficulties) at the Kylerec 2017 tab at this link. Other notes (with shorter load times, and including the ones I’m missing) ~~will be posted on the Kylerec website soon~~ are now posted on the Kylerec website here.

Comments and corrections are very welcome!

Definitions

We quickly review the various notions of fillings of a contact manifold. We shall always assume that our manifolds are oriented and contact structures cooriented. As a starting point, one might be interested in smooth fillings of contact manifolds. It turns out that this problem is rather uninteresting. Every contact manifold of dimension $2n+1$ has a structure group which can be reduced to $U(n) \times 1$ , but the complex bordism group is well known to satisfy $\Omega^U_{2n+1} = 0$ . As a consequence, every contact manifold is smoothly fillable. We must therefore consider fillability questions which extend beyond the realm of complex bordism in order to discover interesting phenomena.

These notions are as follows, in (strictly!) increasing order of strength.

We say a contact 3-manifold $(M^3,\xi)$ is weakly fillable if it is the smooth boundary of a symplectic manifold $(W^4,\omega)$ such that $\omega|_{\xi} > 0$ . There is a generalization in higher dimensions due to Massot, Niederkrüger, and Wendl, but we omit it here. (Simply requiring that $\omega|_{\xi}$ is ~~a positive symplectic form~~ in the same conformal symplectic class as the natural one on $\xi$ , i.e. is $d\alpha|_{\xi}$ up to scaling where $\alpha$ is a contact form for $\xi$ , implies strong fillability in higher dimensions, by McDuff.)
We say a contact manifold $(M^{2n-1},\xi)$ is strongly fillable if there is a weak filling $(W^{2n},\omega)$ such that one can find a Liouville vector field $V$ in a neighborhood of $M$ , i.e. one such that $\mathcal{L}_V\omega = \omega$ , such that $(\iota_V\omega)|_M$ gives a (properly cooriented) contact form for $\xi$ .
We say a contact manifold $(M^{2n-1},\xi)$ is exactly fillable if there is a strong filling such that the Liouville vector field $V$ can be extended to all of $(W,\omega)$ . In other words, $M$ is the contact boundary of a Liouville domain $(W,\omega = d\alpha)$ where $\alpha = \iota_V\omega$ .
We say a contact manifold $(M^{2n-1},\xi)$ is Weinstein (or Stein) fillable if it is exactly fillable by some $(W,\omega = d\alpha)$ , where $\alpha = \iota_V\omega$ , such that there is also a Morse function $f$ on $W$ such that $V$ is gradient-like for $f$ and $M$ is a maximal regular level set. In other words, $M$ is the contact boundary of a Weinstein domain.

As a final remark, there is a notion of overtwistedness in contact manifolds. In 3-dimensions, this is characterized by the existence of an overtwisted disk. This was known to obstruct all types of fillings, due to Eliashberg and Gromov. In higher dimensions, overtwistedness was defined in a paper of Borman, Eliashberg, and Murphy, which was discussed on this blog by Laura Starkston and Roger Casals, starting with this post and concluding with this one. This definition implies the existence of a plastikstufe as defined by Niederkrüger, which had been already shown to obstruct fillings (strongly in the same paper, weakly in the paper by Massot, Niederkrüger, and Wendl). In other words, in any dimension, overtwistedness implies not fillable. A contact manifold which is not overtwisted is called tight, so equivalently, fillable implies tight, in all dimensions.

To summarize this section:

Tight < Weakly fillable < Strongly fillable < Exactly fillable < Weinstein fillable

where all of the inclusions turn out to be strict.

Two Motivating Questions

Question 1: What tools do we have at each level of fillability?

The easiest type of filling to understand is that of the Weinstein filling, since Weinstein domains have an explicit surgery theory, which lends themselves to concrete geometric descriptions. Most notably, a Weinstein domain can be thought of as a symplectic Lefschetz fibration, which naturally has an open book decomposition on its boundary whose monodromy is a product of positive Dehn twists. Hence, Weinstein fillings and fillability can be studied through studying supporting open book decompositions for a contact manifold $(M,\xi)$ .

Another rather powerful tool is the study of J-holomorphic curves. Let us provide a quick example: the proof that fillability of a contact 3-manifold implies tightness. One assumes by way of contradiction that an overtwisted contact 3-manifold has a filling. Then one considers a certain compact 1-dimensional moduli space of J-holomorphic curves with boundary on the overtwisted disk. One finds an explicit component of this moduli space which has one endpoint (a constant disk) but cannot have another endpoint, which contradicts the compactness of the moduli space. In higher dimensions, studying similar moduli spaces of J-holomorphic curves yields obstructions to fillings.

There are some other miscellaneous techniques. For example, Liouville domains have attached to them a symplectic homology, which provides another tool for the case of exact fillings. And in the case of 3-dimensional contact manifolds, one can also study the Seiberg-Witten invariants of a given filling.

Question 2: How can we study the topology of different fillings? Or tell when fillings are distinct even if they have the same homology?

J-holomorphic curves come with extra evaluation maps which allow one to study how the moduli space of curves compares to some underlying topology, e.g. of the filling or of the contact manifold. This is a technique which comes up many times in different contexts, and it sometimes allows us to produce maps between the filling or the contact manifold in question which do not exist for any other obvious reason.

Similarly, symplectic homology in its two flavors $SH$ and $SH^{+}$ fits into an exact triangle with Morse homology, and so one can understand the topology of a filling from its symplectic homology. One might be interested, for example, in studying fillings with $SH = 0$ , in which case the homology of the filling is completely determined by $SH^{+}$ . Alternatively, $SH$ can be used directly to distinguish fillings.

Overview of Kylerec

More detailed posts about the contents of Kylerec will appear in future blog posts, but I will outline here precisely what was covered.

Day 1: After an overview talk, we spent the rest of the day studying the surgery theory of Weinstein manifolds, and began our study of the correspondence between Weinstein fillings, Lefschetz fibrations, and open book decompositions.

Day 2: We highlighted some results from this correspondence, and then turned towards an introduction to the theory of J-holomorphic curves, including applications of this theory to fillings via McDuff’s classification result as well as Wendl’s J-holomorphic foliations.

Day 3: On our short day, we first discussed some applications of J-holomorphic curves to high-dimensional fillings due to Barth, Geiges, and Zehmisch (for example reproving the result of Eliashberg, Floer, and McDuff that the standard sphere has a unique aspherical filling), and applied Wendl’s theorem (as discussed in Day 2) following a paper of Plamenevskaya and Van Horn-Morris to show that many contact structures on the lens spaces $L(p,1)$ have unique Weinstein fillings up to deformation equivalence.

Day 4: We discussed the Seiberg-Witten equations, how they appear in symplectic geometry, and how they are used by Lisca and Matic to distinguish contact structures on homology 3-spheres which are homotopic (through plane fields) but not isotopic (through contact structures). We also discussed how Calabi-Yau caps, as defined by Li, Mak, and Yasui, can be used to prove certain uniqueness results on fillings of unit cotangent bundles of surfaces, as in this paper by Sivek and Van Horn-Morris.

Day 5: On our last day, we focused mainly on symplectic homology (and its variants). In one talk, we performed computations which allowed us to distinguish contact structures on standard spheres (see Ustilovsky’s paper) and to compute the symplectic homology of fillings of certain Brieskorn spheres (see Uebele’s paper). We also discussed Lazarev’s generalization of M.-L.Yau’s theorem (that subcritical Weinstein fillings have isomorphic integral cohomology) to the flexible case.

5 Comments

Filed under Uncategorized

Monthly Archives: June 2017

Kylerec – On J-holomorphic curves, part 2

A preparatory comment on last time

On Wendl’s Strongly fillable contact manifolds and J-holomorphic foliations

On Barth-Geiges-Zehmisch’ The diffeomorphism type of fillings

Kylerec – On J-holomorphic curves, part 1

J-holomorphic curves – basics

A first example – Fillable implies tight (in 3 dimensions)

On McDuff’s The structure of ruled and rational symplectic 4-manifolds

Kylerec Overview

Definitions

Two Motivating Questions

Overview of Kylerec

Recent Posts

Archives

Categories

Meta