This is my summary of Yasha Eliashberg’s minicourse. The topic is contact and symplectic homology invariants of Weinstein manifolds, and the effects of handle attachments. I think the theories are too complicated to explain all the details in 3 talks, so if you really want to compute these things, look at the paper by Bourgeois, Ekholm, and Eliashberg here: http://arxiv.org/pdf/0911.0026v4.pdf
Part I: Weinstein manifolds
The goal is to compute invariants of Weinstein manifolds. A Weinstein manifold consists of the following data:  where
where
–  is an exact symplectic manifold with primitive
is an exact symplectic manifold with primitive  (
( )
)
– Z is a complete vector field such that  (note Z and
(note Z and  determine the primitive
determine the primitive  )
)
–  is an exhausting function (proper and bounded below)
is an exhausting function (proper and bounded below)
– Z is gradient-like for 
Note that  and
and  is equivalent to
is equivalent to 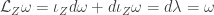 . We say in this case that Z is a Liouville vector field. Also note, X is necessarily noncompact since it is an exact symplectic manifold (Stokes theorem).
. We say in this case that Z is a Liouville vector field. Also note, X is necessarily noncompact since it is an exact symplectic manifold (Stokes theorem).
We will restrict to Weinstein manifolds of finite type, meaning  has finitely many critical points. This means that there is some regular value c, such that all critical values are less than c. In this case,
has finitely many critical points. This means that there is some regular value c, such that all critical values are less than c. In this case,  has a conical end,
has a conical end,  . Therefore it is frequently interesting to just look at
. Therefore it is frequently interesting to just look at ![\overline{X}=\phi^{-1}((-\infty, c])](https://s0.wp.com/latex.php?latex=%5Coverline%7BX%7D%3D%5Cphi%5E%7B-1%7D%28%28-%5Cinfty%2C+c%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) , such things are called Weinstein domains. One can also consider Weinstein cobordisms:
, such things are called Weinstein domains. One can also consider Weinstein cobordisms: ![\phi^{-1}([c_1,c_2])](https://s0.wp.com/latex.php?latex=%5Cphi%5E%7B-1%7D%28%5Bc_1%2Cc_2%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) for regular values
for regular values 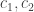 .
.
For any regular level set of the Weinstein structure function  , the restriction of
, the restriction of  is a contact form:
is a contact form:  must be positive on a basis for
must be positive on a basis for  since the span of Z is the kernel of
since the span of Z is the kernel of  , and Z is transverse to the regular level sets.
, and Z is transverse to the regular level sets.
There is some question of whether you can generally perturb the Weinstein structure to ensure  is a Morse function, but in the case where it is Morse, you can consider the stable manifold of a critical point. Such stable manifolds are isotropic for both
is a Morse function, but in the case where it is Morse, you can consider the stable manifold of a critical point. Such stable manifolds are isotropic for both  and
and  (i.e. the restriction of the primitive to the stable manifold is zero). This implies that the indices of all critical points of
(i.e. the restriction of the primitive to the stable manifold is zero). This implies that the indices of all critical points of  are at most half the dimension of X. The intersection of the level sets with the stable manifolds are isotropic in the contact sense.
are at most half the dimension of X. The intersection of the level sets with the stable manifolds are isotropic in the contact sense.
A question we would like to understand is how does the Weinstein manifold change as we pass through critical points of  . Topologically we are doing a handle attachment, and the geometric information we get is that the attaching sphere will be isotropic in the contact sense, and the core of the handle will be isotropic in the symplectic sense. The framing on a Legendrian attaching sphere (for middle dimensional handles) is completely determined when the contact structure is co-oriented.
. Topologically we are doing a handle attachment, and the geometric information we get is that the attaching sphere will be isotropic in the contact sense, and the core of the handle will be isotropic in the symplectic sense. The framing on a Legendrian attaching sphere (for middle dimensional handles) is completely determined when the contact structure is co-oriented.
We can understand Weinstein manifolds and their invariants piece by piece for each handle addition. To use this method it is useful to establish a lemma that allows one to reorder the critical points, without meaningfully changing the Weinstein structure. One main reason for this is that all of the interesting symplectic geometry happens when attaching the n handles in a 2n dimensional manifold, so we want to attach all the k<n handles first and then focus on what happens when attaching the n-handles. Here, noninteresting means that h-cobordism principles hold, so information about the tangent bundle determines the symplectic manifold. There are also certain Legendrian attaching spheres (called loose) for n-handles for which the Weinstein manifold is determined homotopically (information about the tangent bundle determines the symplectic manifold).
Part II: Invariants of Weinstein manifolds: Symplectic and Contact homology
Set up: Let  be a Weinstein manifold of finite type,
be a Weinstein manifold of finite type, ![\overline{X}=\phi^{-1}((-\infty,c])](https://s0.wp.com/latex.php?latex=%5Coverline%7BX%7D%3D%5Cphi%5E%7B-1%7D%28%28-%5Cinfty%2Cc%5D%29&bg=ffffff&fg=333333&s=0&c=20201002) be a Weinstein domain such that X is
be a Weinstein domain such that X is  union a conical end, and let
union a conical end, and let  . We will build up some chain complexes that are invariants of the Weinstein manifold X.
. We will build up some chain complexes that are invariants of the Weinstein manifold X.
Reeb orbits: the first basic generators of the chain complex will be Reeb chords and periodic orbits of the Reeb vector field associated to  on Y. It is convenient for the following to assume
on Y. It is convenient for the following to assume  . For each periodic Reeb orbit there is a Conley-Zehnder index, there is also a well-defined index associated to Reeb chords. There is some distinction between “good” Reeb orbits and “bad” ones. A bad Reeb orbit is an even multiple of another Reeb orbit, such that the parity of the Conley-Zehnder index can change as one takes different multiples of the simple Reeb orbit. Orbits that are not bad are good. These bad orbits introduce some additional problems one needs to compensate for to get a well defined theory.
. For each periodic Reeb orbit there is a Conley-Zehnder index, there is also a well-defined index associated to Reeb chords. There is some distinction between “good” Reeb orbits and “bad” ones. A bad Reeb orbit is an even multiple of another Reeb orbit, such that the parity of the Conley-Zehnder index can change as one takes different multiples of the simple Reeb orbit. Orbits that are not bad are good. These bad orbits introduce some additional problems one needs to compensate for to get a well defined theory.
Linearized contact homology  : While this invariant is meant to give information about the contact manifold Y, it depends on the choice of a Weinstein filling X. The chain complex for linearized contact homology is generated (over some field of characteristic 0) by the set of all good Reeb orbits.
: While this invariant is meant to give information about the contact manifold Y, it depends on the choice of a Weinstein filling X. The chain complex for linearized contact homology is generated (over some field of characteristic 0) by the set of all good Reeb orbits.
The differential for contact homology: The coefficient 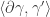 is a count of holomorphic “cylinders” in the symplectization of Y connecting
is a count of holomorphic “cylinders” in the symplectization of Y connecting  to
to  . The quotations are because we must count curves that have additional ends on the negative end besides just
. The quotations are because we must count curves that have additional ends on the negative end besides just  , when these additional ends can be capped of by holomorphic disks in the filling
, when these additional ends can be capped of by holomorphic disks in the filling 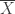 , of Y. These curves are called cylinders anchored in the symplectic filling.
, of Y. These curves are called cylinders anchored in the symplectic filling.

Note that this is where the dependence on X for contact homology comes from. Counting these anchored cylinders is necessary to get the differential to square to zero since these appear as ends of the moduli space.
Reduced Symplectic Homology,  : While contact homology ignores the bad vertices, we can obtain additional information by including the bad vertices and compensating for their bad behavior in the differential. To do this we take two direct sum copies of the module generated by all Reeb orbits. We indicate orbits are in the first copy by putting a check over them, and in the second copy by putting a hat over them. Additionally, the elements in the second copy have grading shifted by 1.
: While contact homology ignores the bad vertices, we can obtain additional information by including the bad vertices and compensating for their bad behavior in the differential. To do this we take two direct sum copies of the module generated by all Reeb orbits. We indicate orbits are in the first copy by putting a check over them, and in the second copy by putting a hat over them. Additionally, the elements in the second copy have grading shifted by 1.  , where
, where 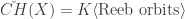 and
and ![\widehat{CH}(X) = K\langle \text{Reeb orbits}\rangle[1]](https://s0.wp.com/latex.php?latex=%5Cwidehat%7BCH%7D%28X%29+%3D+K%5Clangle+%5Ctext%7BReeb+orbits%7D%5Crangle%5B1%5D&bg=ffffff&fg=333333&s=0&c=20201002) .
.
The differential for plus symplectic homology: Since there are two direct summands in the chain complex 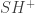 , we write the differential in block matrix form:
, we write the differential in block matrix form:
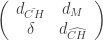 .
.
Here 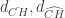 are the differentials defined previously for CH by counting anchored cylinders.
are the differentials defined previously for CH by counting anchored cylinders. 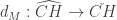 sends good hat orbits to zero, and for a bad orbit
sends good hat orbits to zero, and for a bad orbit  (this has something to do with the parity issues that bad orbits have). For each Reeb orbit, we will keep track of a marked point (so we have more data about the parametrization). The map
(this has something to do with the parity issues that bad orbits have). For each Reeb orbit, we will keep track of a marked point (so we have more data about the parametrization). The map  counts holomorphic cylinders where the marks on the two Reeb orbits are aligned in the product, and also broken cylinders where the marked points show up in a chosen cyclic order as in the below picture.
counts holomorphic cylinders where the marks on the two Reeb orbits are aligned in the product, and also broken cylinders where the marked points show up in a chosen cyclic order as in the below picture.

Note that both of these are counts of a moduli space one codimension higher than the moduli space of unrestricted cylinders. I’m assuming all of these maps defined via counting curves are just summing over the 0-dimensional moduli spaces (or 1-dimensional moduli spaces mod an R-action).
Full Symplectic Homology,  : For this theory, we combine the symplectic homology chain complex which keeps track of Reeb orbits and holomorphic cylinders connecting them, with the Morse chain complex for
: For this theory, we combine the symplectic homology chain complex which keeps track of Reeb orbits and holomorphic cylinders connecting them, with the Morse chain complex for  , which keeps track of the handle attachments. The chain complex is given by
, which keeps track of the handle attachments. The chain complex is given by ![SH(X) = SH^+(X) \oplus Morse(-\phi)[-n]](https://s0.wp.com/latex.php?latex=SH%28X%29+%3D+SH%5E%2B%28X%29+%5Coplus+Morse%28-%5Cphi%29%5B-n%5D&bg=ffffff&fg=333333&s=0&c=20201002) , where
, where 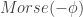 is the Morse chain complex generated by critical points of
is the Morse chain complex generated by critical points of  , whose differential counts gradient flowlines between critical points.
, whose differential counts gradient flowlines between critical points.
The differential for symplectic homology can again be defined by a block matrix in terms of the two summands:
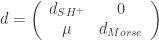
where here ![\mu: SH^+(X) =\check{CH}(X) \oplus \widehat{CH}(X) \to Morse(-\phi)[-n]](https://s0.wp.com/latex.php?latex=%5Cmu%3A+SH%5E%2B%28X%29+%3D%5Ccheck%7BCH%7D%28X%29+%5Coplus+%5Cwidehat%7BCH%7D%28X%29+%5Cto+Morse%28-%5Cphi%29%5B-n%5D&bg=ffffff&fg=333333&s=0&c=20201002) is defined by
is defined by 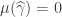 and
and  where
where  counts the number of holomorphic disks bounding
counts the number of holomorphic disks bounding 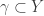 whose center marked point maps into the stable manifold of p.
whose center marked point maps into the stable manifold of p.
Note that since the differential for SH is lower-triangular, there is a short exact sequence of the complexes:  which induces an exact triangle on the level of homology:
which induces an exact triangle on the level of homology: 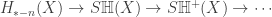 .
.
For 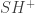 , there is not quite an exact triangle between
, there is not quite an exact triangle between  since the differential is not triangular, so neither inclusions of
since the differential is not triangular, so neither inclusions of  or
or  into
into 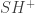 are chain maps. However since the map $d_M$ is zero on good orbits, we get an exact triangle
are chain maps. However since the map $d_M$ is zero on good orbits, we get an exact triangle  when all Reeb orbits are good.
when all Reeb orbits are good.
Part III: Computing Contact and Symplectic Homology
We want to compute these invariants via handlebody decompositions. Therefore we would like to know what the effect of attaching handle has on the Contact/Symplectic homology. The effects of adding subcritical handles (index <n) are basically trivial (the symplectic homology vanishes for Weinstein manifolds built from handles of index <n). Therefore we look at what happens to these homology invariants when attaching n-handles.
In the Weinstein manifold, the attaching spheres of the n-handles will be Legendrian submanifolds of the level set Y. There is an algebraic construction that captures the contribution of the n-handle to contact/symplectic homology in terms of the Legendrian attaching sphere. The construction is essentially a differential polynomial algebra  generated by the Reeb chords, with some extra formal variables added in. The differential is computed by correctly counting holomorphic disks with boundary along the Legendrian except at finitely many punctures which map to the Reeb chords. The details are probably more accurately described in the paper by Bourgeois, Ekholm, and Eliashberg, but the point is that there is a clear prescription on how to compute this once you understand the Reeb chords and some holomorphic disk counts of the Legendrian attaching sphere.
generated by the Reeb chords, with some extra formal variables added in. The differential is computed by correctly counting holomorphic disks with boundary along the Legendrian except at finitely many punctures which map to the Reeb chords. The details are probably more accurately described in the paper by Bourgeois, Ekholm, and Eliashberg, but the point is that there is a clear prescription on how to compute this once you understand the Reeb chords and some holomorphic disk counts of the Legendrian attaching sphere.
Now suppose  where h is an n-handle attached along a Legendrian
where h is an n-handle attached along a Legendrian 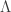 . The theorem is that we get the complex for X, from the complex for
. The theorem is that we get the complex for X, from the complex for 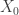 and
and  ,
,  and the differential is given in block matrix form by
and the differential is given in block matrix form by
 .
.
Here the map  is zero on the hat part of SH. On the check part it counts holomorphic punctured disks, which send the puncture in the center asymptotically to the Reeb orbit
is zero on the hat part of SH. On the check part it counts holomorphic punctured disks, which send the puncture in the center asymptotically to the Reeb orbit  , and maps the boundary of the disk to the Legendrian, except along finitely many points which map to Reeb chords showing up as a term in
, and maps the boundary of the disk to the Legendrian, except along finitely many points which map to Reeb chords showing up as a term in  . (There is also a particular ray from
. (There is also a particular ray from  to the boundary, which is kept track of through the formal structure of
to the boundary, which is kept track of through the formal structure of  .) Finally on the Morse summand of the SH complex,
.) Finally on the Morse summand of the SH complex,  counts some holomorphic disks that intersect the stable manifold of a critical point.
counts some holomorphic disks that intersect the stable manifold of a critical point.
The payoff here is that there is an exact triangle relating  . In the case that
. In the case that 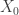 has only handles of index <n, its symplectic homology vanishes, so we get an isomorphism
has only handles of index <n, its symplectic homology vanishes, so we get an isomorphism  . There are some additional techniques to obtain the computations of
. There are some additional techniques to obtain the computations of  that involve looking at the corresponding algebra for the boundary of the cocore instead of the attaching sphere, and looking at some linearizations using augmentations handed to you by the Lagrangian filling of the Legendrian. Eliashberg thinks that such invariants are reasonable to compute, though that probably assumes one knows a lot about counting various kinds of holomorphic curves.
that involve looking at the corresponding algebra for the boundary of the cocore instead of the attaching sphere, and looking at some linearizations using augmentations handed to you by the Lagrangian filling of the Legendrian. Eliashberg thinks that such invariants are reasonable to compute, though that probably assumes one knows a lot about counting various kinds of holomorphic curves.







