Overtwisted disks and filling holes

This post is on the end of the proof by Borman, Eliashberg, and Murphy that there is an overtwisted contact structure in every homotopy class of almost contact structures in higher dimensions and via the parametric version, any two overtwisted contact structures which are homotopic as almost contact structures, are isotopic as contact structures. There are a number of other posts preceding this one that are meant to be read first, and there are a few pieces of the proof that we skipped, but I think this will be my last post on this topic.

Overtwisted disks in higher dimensions and filling the holes

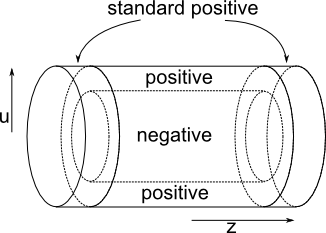
In dimension three, an overtwisted disk is a certain model germ of a contact structure on a two dimensional disk. The key property of this overtwisted disk which generalizes in higher dimensions, is its role in the proof of the h-principle: after connecting the codimension zero “holes” where the almost contact structure resists becoming genuinely contact, with a neighborhood of the overtwisted disk, one is able to extend the contact structure. One useful feature of overtwisted disks in dimension three, is that they can be recognized simply by finding an embedded unknotted circle with Thurston-Bennequin number 0 (the contact planes along the unknot do not twist relative to the Seifert framing determined by the disk that is bounded by the unknot). This is not true in higher dimensions: there are quantitative properties of the contact structure on the interior of the disk which are needed for the h-principle proof to work.

Recall, from Roger’s post, that in the presence of an overtwisted disk, we can reduce the problem of extending the contact structure over the hole, to extending the contact structure over an annulus (interval times sphere) whose germ on one boundary component is modelled by the contact Hamiltonian obtained by concatenating the Hamiltonian modelling the hole with the overtwisted model Hamiltonian, and whose germ on the other boundary component is given by the overtwisted Hamiltonian. (Remember this picture?)

This is because we can connect each hole to an overtwisted annulus by a tunnel, and then forget that we already had a genuine contact structure on the tunnel and the overtwisted annulus and just look at the contact germs on the two boundary components of the boundary sum of the ball with the annulus, like in this schematic picture.

This is the key point where we use the overtwistedness of the contact structure. The arguments to get to this point are made in a relative way that just fixes the contact structure in the overtwisted regions. At this point, we need to change the contact structure on the overtwisted annulus. In order to fill in the larger annulus (the overtwisted annulus connected to the hole) with a genuine contact structure, we need to show that, up to conjugation, the overtwisted Hamiltonian is less than the connect sum of the Hamiltonian for the hole with the overtwisted Hamiltonian. We are assuming at this point, that we know how to homotope the almost contact structure so that it is genuinely contact in the complement of holes, and each of the holes has its almost contact structures given by a circle model. Moreover, by doing this extra carefully (using equivariant coverings), we can assume that there are finitely many different types of contact Hamiltonians defining the circle models for the holes. The number of types of contact Hamiltonians needed a priori depends on the dimension. An easier reduction is to assume that the Hamiltonian $K: \Delta\times S^1 \to \mathbb{R}$ is independent of the $S^1$ (time) direction since the circle is compact so $\overline{K}(x)=\min_{\theta\in S^1} K(x,\theta)$ is well-defined and satisfies $\overline{K}\leq K$ so there is a genuine contact annulus extending the contact structure from the boundary of the circle model for $K$ inward to the boundary of the circle model for $\overline{K}$ .

In order to prove the key lemma that we can fill in the appropriate annuli, we need a more concrete family of contact Hamiltonians. Consider a contact Hamiltonian $K_{\varepsilon}$ on the cylinder $\Delta_{cyl}=\{(z,u_i,\theta_i): |z|\leq 1, u=\sum u_i\leq 1\}\subset \mathbb{R}^{2n-1}$ which is negative on the region where $|z|$ and $u$ are both less than $1-\varepsilon$ , and which increases linearly from 0 in $z$ and $u$ towards the boundary with slope 1. These are called special Hamiltonians . The main thing which is special about such a Hamiltonian $K_{\varepsilon}$ is that there is a contact embedding $\Theta$ of $\Delta_{cyl}$ with the standard contact form, into the boundary sum of $\Delta_{cyl}$ with itself, such that $\Theta_*K_{\varepsilon}$ is less than the connected sum of $K_{\varepsilon}$ with itself. Given this, if the hole and the overtwisted annulus are both modelled by such Hamiltonians with the same $\varepsilon$ , we can fill in the holes by genuine contact structures.

Notice that any contact Hamiltonian which is positive on $\partial \Delta_{cyl}$ must dominate (is greater than) some special Hamiltonian for sufficiently small $\varepsilon$ . It is important that it is possible to reduce to assuming that the holes are modelled by finitely many types of contact Hamiltonian circle models, therefore in a given dimension, there is a certain universal $\varepsilon_{univ}$ , such that for any $\varepsilon<\varepsilon_{univ}$ , every hole dominates a circle model for a special $K_{\varepsilon}$ . Therefore, the key overtwisted annuli are given by circle models for special Hamiltonians corresponding to such an $\varepsilon$ .

To get from overtwisted annuli to overtwisted disks, we use the fact that the main lemma embedding $\Theta$ fixes the end where $z\in[1-\varepsilon,1]$ . Therefore we do not need the full annulus (neighborhood the boundary of the cylinder), only the topological disk obtained but cutting off the end of the cylinder.

The overtwisted disk is thus defined to be the disk with the contact germ on the boundary of a circle model over a cylinder (excluding one end) defined by a special contact Hamiltonian $K_{\varepsilon}$ for some $\varepsilon<\varepsilon_{univ}$ where $\varepsilon_{univ}$ depends only on the dimension. I think that dependence on the dimension is not really understood at this point, but the idea is that $\varepsilon_{univ}$ probably gets smaller as the dimension increases, so the region where the contact Hamiltonian is negative would be larger.

Proving the main lemma

We want to show that there is a contact embedding $\Theta:\Delta_{cyl}\to \Delta_{cyl}\# \Delta_{cyl}$ such that for a special Hamiltonian $K_{\varepsilon}$ , $\Theta_*K_{\varepsilon}<K\# K$ (where here $\#$ denotes the boundary sum obtained by tubing the two cylinders together so that the contact Hamiltonian is positive on the tube). For the parametric version, the main lemma shows there is a family $\Theta_s$ interpolating between the identity and $\Theta$ .

Recall the things we know how to do with contactomorphisms from the previous post:
(1) We can reorder contact Hamiltonians however we want in regions where they are negative by the disorder lemma.
(2) We have transverse scaling contact embeddings which shrinks/expands $\Delta_{cyl}$ in the $z$ direction by a diffeomorphism $h:\mathbb{R}\to \mathbb{R}$ at the cost of correspondingly shrinking/expanding $\Delta_{cyl}$ in the $u$ direction by rescaling by $h'(z)$ . The effect on the contact Hamiltonian is $(\Phi_h)_*K(h(z),h'(z)u,\theta)=h'(z)K(z,u,\theta)$ .
(3) We have twist embeddings which shrink/expand $\Delta_{cyl}$ in the radial $u$ direction by rescaling by $\frac{1}{1+g(z)u}$ if you allow the angular $\theta$ directions to be twisted. The effect on the contact Hamiltonian if we ignore the angular coordinate is $(\Psi_g)_*K(z,\frac{u}{1+g(z)u})=(1-g(z)u)K(z,u)$ .

To prove the main lemma, we want to stretch out the $z$ direction of $\Delta_{cyl}$ so that it spreads the length of the connected sum. We can do this with a transverse scaling contactomorphism, but the $u$ directions will expand: $(z,u)\mapsto (h(z),h'(z)u)$ . Since we don’t want to mess with the contact structure on the $z$ ends, we choose $h$ to look like a translation so $h'(z)=1$ when $z$ is within $\varepsilon$ of the ends. We can compensate for the expansion in the $u$ directions away from the ends with a twist embedding which rescales the expanded $u$ directions to fit back inside a (longer) cylinder where $u\leq 1$ , by choosing $g(z)=1-\frac{1}{h'(h^{-1}(z))}$ . The total effect of composing these two maps is an embedding $\Gamma$ mapping $(z,u)\mapsto (h(z),\frac{h'(z)u}{1+(h'(z)-1)u})$ (the angular directions get twisted some amount but we don’t care). $\Gamma$ sends a short cylinder $\Delta_{cyl}$ to a longer cylinder $\Delta_{cyl}\# \Delta_{cyl}$ , so that the points where $u=1$ are sent to points where $u=1$ , but points where $u<1$ are sent to points with $u$ -coordinate $\frac{h'(z)u}{1+(h'(z)-1)u}> u$ . So this contactomorphism inflates the cylinder in the $u$ directions towards the boundary. By choosing a family of diffeomorphisms $h_s$ starting with a basic translation we get a family of embeddings $\Gamma_s$ which look like this:

Now, we want to see the effect on the contactomorphisms on a special Hamiltonian $K_{\varepsilon}$ . We find that

$(\Gamma_s)_*K_{\varepsilon}(h_s(z),\frac{h_s'(z)u}{1+(h_s'(z)-1)u})=(h_s'(z)-(h_s'(z)-1)u)K(z,u)$

which can be rewritten as

$(\Gamma_s)_*K_{\varepsilon}(h_s(z),u)=(h_s'(z)-(h_s'(z)-1)u)K\left(z,\frac{u}{h_s'(z)-(h_s'(z)-1)u}\right)$ .

When $z$ is within $\varepsilon$ of the ends, we have chosen $h$ to be a translation, so $(\Gamma_s)_*K_{\varepsilon}(h_s(z),u)=K_{\varepsilon}(z,u)$ , i.e. the Hamiltonian is basically fixed to be standard on these ends. When we reach $s=1$ , the ends of $\Gamma_1(\Delta_{cyl})$ coincide with the ends of $\Delta_{cyl}\#\Delta_{cyl}$ so in these regions $(\Gamma_1)_*(K_\varepsilon)=K_{\varepsilon}\#K_{\varepsilon}$ .

The rescaling factor for the Hamiltonian, $(h_s'(z)-(h_s'(z)-1)u)$ is always greater than or equal to 1, so the region where $(\Gamma_s)_*K \leq 0$ is the image under $\Gamma_s$ of the region where $K\leq 0$ and similarly $\{(\Gamma_s)_*K\geq 0\}=\Gamma_s(\{K\geq 0\})$ . Since we can use the disorder lemma, we don’t care much about the exact negative values of $(\Gamma_s)_*K$ , but we do need $(\Gamma_1)_*K(z,u)\leq K\#K(z,u)$ wherever $(\Gamma_1)_*K\geq 0$ . Therefore we need to check this inequality on points $\Gamma_1(z,u)$ where $u\in [1-\varepsilon,1]$ and $z$ is more than $\varepsilon$ away from the ends (since we already understand the behavior when $z$ is within $\varepsilon$ of the boundary). On this region, the special Hamiltonian $K_{\varepsilon}$ is just a linear function of $u$ with slope 1. Therefore

$(\Gamma_s)_*K_{\varepsilon}(h_s(z),u)=(h_s'(z)-(h_s'(z)-1)u)\left(\frac{u}{h_s'(z)-(h_s'(z)-1)u}-(1-\varepsilon) \right)$

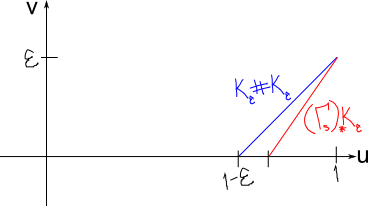
which as a function of $u$ is linear, has the value $0$ when $\frac{u}{h_s'(z)-(h_s'(z)-1)u}=1-\varepsilon$ , and the value $\varepsilon$ at $u=1$ . Notice that $\frac{u}{h_s'(z)-(h_s'(z)-1)u}=1-\varepsilon$ when $u=\frac{h_s'(z)(1-\varepsilon)}{1+(h_s'(z)-1)(1-\varepsilon)}>1-\varepsilon$ so in this region $(\Gamma_s)_*K_{\varepsilon}$ compares to $K\#K$ like this:

Therefore $(\Gamma_1)_*K_{\varepsilon}(z,u)\leq K\#K(z,u)$ wherever $(\Gamma_1)_*K_{\varepsilon}\geq 0$ . Then we can use the disorder lemma to produce a contactomorphism which fixes everything on this positive region but makes the Hamiltonian sufficiently negative in the region where $K_\varepsilon\#K_\varepsilon\leq 0$ so that after composing $\Gamma_s$ with this disorder contactomorphism we get the embedding $\Theta_s$ such that $(\Theta_1)_*K_{\varepsilon}\leq K_{\varepsilon}\#K_{\varepsilon}$ as required. Notice that $\Theta_s$ fixes the end where $z\in[1-\varepsilon,1]$ so we do not actually need to use that end of the overtwisted annulus to fill in the hole.

It is worth noting that an overtwisted disk could be modelled using any Hamiltonian for which the main lemma could be proven, not just the ones that increase linearly near the boundary. The tricky part to check for a more general function is the inequality near the $u$ -boundary. When the contact Hamiltonian was linear, the contactomorphism transformation and the rescaling factor cancelled in just the right way so that the pushed forward contact Hamiltonian was still linear in $u$ so the inequality could be determined simply by understanding the values near end points. For more general contact Hamiltonians you would probably need to do more work to get the required estimates.

Overtwisted disks and filling holes

One response to “Overtwisted disks and filling holes”

Leave a comment Cancel reply

Recent Posts

Archives

Categories

Meta

Overtwisted disks and filling holes

Share this:

Related

One response to “Overtwisted disks and filling holes”

Leave a comment Cancel reply

Recent Posts

Archives

Categories

Meta