News from University of Minnesota 4-manifolds workshop

I am writing from the 4-manifolds conference at the University of Minnesota. Lots of different approaches to and constructions of 4-manifolds have been discussed and slides from some of the courses are on the conference website . Today, I want to focus on Chris Wendl’s mini-course on characterizing symplectic fillings of certain contact structures (supported by a spinal open book with a planar page) in terms of Lefschetz fibrations. Additionally, the different notions of symplectic filling (weak, strong, Liouville, Weinstein, or Stein – see my previous post and Chris’ comment for details on these variations) all coincide in this case (up to blowing up). The results are contained in a paper of Lisi, Van Horn-Morris and Wendl coming out soon. This generalizes Chris’ earlier paper on the analogous theorem for regular planar open book decompositions . The results seem really powerful if one can make sense of how to find good spinal open books supporting contact manifolds of interest.

Though there may be some similarly defined notions in high dimensions, these results are only for 4-manifolds with 3-manifold boundary.

The definition for a spinal open book is motivated by looking at the decomposition induced on the boundary of a Lefschetz fibration. A Lefschetz fibration on a 4-manifold $E$ , is a smooth map to a surface $\Sigma$ , $\pi: E\to \Sigma$ which has finitely critical points so that each critical point has a coordinate neighborhood so that $\pi$ in these coordinates looks like $(z_1,z_2)\mapsto z_1^2+z_2^2$ where $z_1,z_2$ are complex coordinates. The base surface $\Sigma$ and the generic fibers can have many boundary components, but $\Sigma$ should have at least one boundary component if we want to study Lefschetz fibrations of manifolds with boundary. It is useful, particularly when defining spinal open book decompositions, to choose $E$ to be a manifold with corners so that you can think of the fibers as sitting vertically and the sections to lie horizontally. Then the boundary decomposes into a horizontal piece and a vertical piece which meet at a codimension 2 corner. In the case with corners it is more accurate to use the term bordered Lefschetz fibration and one needs to be a little careful when talking about smooth maps/structures near the corners.

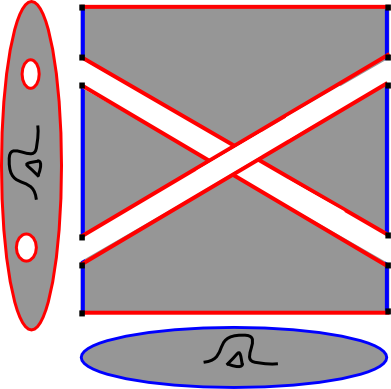
In this schematic picture the red horizontal boundary forms an $S^1$ bundle over three disjoint copies of the base surface $B$ (one for each boundary component of the fiber). This fibration makes up the “spine” of the induced spinal open book decomposition. [Note since $B$ has boundary this fibration is always trivial in this dimension.] The blue vertical boundary forms a $F \sqcup F$ fibration over $S^1$ (one copy of the fiber surface $F$ for each boundary component of the base $B$ ). This fibration is called the paper of the spinal open book decomposition. Each connected component of a fiber in this piece is called a page.

A special case of this is when the base surface is a disk. Then the induced spinal open book on the boundary is a genuine open book decomposition. The spine part is an $S^1$ bundle over $\sqcup_k D^2$ (solid tori forming the binding), and the paper is a surface bundle over the circle with connected fibers (since the number of connected components in a fiber corresponds to the number of boundary components in the base surface $D^2$ ) so each fiber forms the page of an open book decomposition.

In general a spinal open book is a decomposition of a 3-manifold into the spine: any $S^1$ fibration over any surface $\Sigma$ with boundary (not necessarily connected), and the paper: any surface (with boundary and possibly disconnected) bundle over $S^1$ so that the intersection of the spine and the paper is a union of 2-dimensional tori. Many of these spinal open book decompositions do not arise as the boundary of bordered Lefschetz fibrations. However there are some slightly more complicated ways spinal open book decompositions can be found on the boundary of a bordered Lefschetz fibration than the above picture indicates. One thing that can happen is that the base surface of the spine may be a nontrivial cover of the base of the Lefschetz fibration. Maybe the schematic for this looks something like this:

The spine (red part) of the spinal open book decomposition can be a circle bundle over a nontrivial (in this picture double) cover of the base surface of the Lefschetz fibration. One can rule out these sort of Lefschetz fibrations by restricting attention to spinal open book decompositions that are “simple”: for any page, different boundary components of that page touch different components of the spine. In the simple case, a spinal open book whose spine is a circle fibration over a disconnected surface $\Sigma$ must have all connected components of $\Sigma$ be diffeomorphic surfaces. This rules out the existence of Lefschetz fillings for lots of spinal open book decompositions.

The main results of the mini-course were:

Theorem 1 (Decompositions -> Contact/Symplectic Geometry): Spinal open books determine a unique isotopy class of supported contact structures. Bordered Lefschetz fibrations determine a nonempty contractible space of symplectic forms on the 4-manifold which are weak/strong/Stein** fillings of the contact boundary.

**One must assume the bordered Lefschetz fibration is allowable (vanishing cycles are homologically essential) to get this result for Stein fillings.

Theorem 2 (Contact/Symplectic Geometry -> Decompositions): Suppose we have a contact manifold supported by a spinal open book which has a page of genus zero, and a weak symplectic filling of that contact manifold $(W,\omega)$ such that the restriction of $\omega$ to the spinal part of the boundary is exact. Then $(W,\omega)$ is supported by a bordered Lefschetz fibration (determined up to isotopy by the deformation class of $\omega$ ) which induces the given spinal open book decomposition on its boundary.

I will write the compatibility conditions for the contact/symplectic structure with the spinal open book/Lefschetz decomposition, but omit the discussion of the proof of theorem 1 for now.

A contact form $\alpha$ is compatible with a spinal open book decomposition if
(1) $d\alpha$ restricted to the interior of each page is a positive area form
(2) On the spine $\pi_{\Sigma}: M_{\Sigma}\to \Sigma$ , the $S^1$ fibers are Reeb orbits for $\alpha$ .

There is a version of this compatibility notion when you are thinking of the spinal open book decomposition as the boundary of a 4-manifold with corners. In this case you look at germs of 1-forms thought of as the restriction of a smooth 1-form on the 4-manifold to the (not quite smooth) boundary. Require this to be a contact form in the complement of the corner parts between the spine and the paper plus conditions (1) and (2).

The basic compatibility conditions between a bordered Lefschetz fibration of $W$ and a symplectic form $\omega$ which ensure $(W,\omega)$ is a weak symplectic filling are:

(1) The restriction of $\omega$ to each fiber is positive away from critical points
(2) Near critical points $\omega$ tames an almost complex structure $J$ which is defined in advance near each critical point so that the fibers are $J$ holomorphic.
(3) Near the horizontal boundary (spine part) $\omega=d\lambda$ where $\lambda$ is a contact form on the spine compatible with the spinal open book. [This additional partial exactness criterion is special to spinal open book decompositions since it is trivially satisfied for regular open books because the solid tori spines do not support any second cohomology.]

For strong fillings, require $\omega = d\lambda$ near the entire boundary.

The surprising result is theorem 2, the spinal generalization of Wendl’s earlier theorem that characterizes symplectic fillings of contact manifolds supported by planar open books as Lefschetz fillings of that particular open book decomposition. The idea of the proof is to symplectically complete $(W,\omega)$ (attach half of the symplectization to the end), and then fill that completion with a (singular) foliation by $J$ -holomorphic curves.

Symplectic Completions

Given a contact manifold $(M,\xi=\ker(\alpha))$ one can form the symplectization $(\mathbb{R}\times M,\omega =d(e^t\alpha))$ where $t$ is the $\mathbb{R}$ coordinate. In this case the vector field $V=\partial_t$ is Liouville:

$\mathcal{L}_V\omega = d\iota_V(d(e^t\alpha))=d(\iota_V(e^t dt\wedge \alpha +e^t\alpha))=d(e^t\alpha)=\omega$

If a symplectic manifold $(W,\omega)$ has convex boundary $(M,\xi)$ , we can match up a collared neighborhood $N$ of $\partial W=M$ with a piece of this symplectization and form a non-compact symplectic manifold $(\widehat{W},\widehat{\omega})= (W,\omega)\cup_{N} ([0,\infty)\times M,d(e^t\alpha))$ . Similarly for concave boundary one can attach $((-\infty,0]\times M,d(e^t\alpha)$ to a collared neighborhood of the boundary. The advantage of such completions is that the flow of the Liouville vector field no longer runs off the boundary (it’s complete).

Chris discussed a weaker structure than a contact structure one can have near the boundary of a symplectic manifold so that there is still a natural symplectic completion. This is a stable Hamiltonian structure.

A symplectic manifold $(W,\omega)$ has stable boundary if there is a collared neighborhood of $\partial W=M$ identified as $(-\varepsilon,0]\times M$ such that $\ker(\omega|_{\{t\}\times M})$ is independent of $t\in (-\varepsilon,0]$ . This is true if and only if the collared neighborhood is symplectomorphic to $((-\varepsilon,0]\times M, d(e^t\lambda)+\Omega)$ such that:
(1) $d\Omega=0$
(2) $\lambda \wedge \Omega>0$
(3) $\ker(\Omega)\subset \ker(d\lambda)$

In this case $(\lambda,\omega=d(e^t\lambda)+\Omega)$ is called a stable Hamiltonian structure (SHS) on the boundary of $(W,\omega)$ . When $\omega|_M = d\alpha$ for a contact form $\alpha$ , the pair $(\alpha,\omega)$ is a SHS where $\Omega = \omega|_M$ . This is the convex boundary case, where $\partial_t$ gives a Liouville vector field near the boundary. For a general stable Hamiltonian boundary, $\partial_t$ is no longer a Liouville vector field but there is still a natural symplectic structure matching up the boundary to $(\mathbb{R}\times M, d(e^t\lambda)+\Omega)$ .

The advantage of working with completions using stable Hamiltonian structures is that one can work with weak fillings instead of strong fillings and still get the same results as long as the symplectic structure is exact near the spine part of the spinal open book.

Foliating by J-holomorphic curves

We assume for the rest of this post that we have a weak symplectic filling $(W,\omega)$ such that
(1) It weakly fills a contact manifold supported by a planar spinal open book decomposition
(2) On the spine part $M_{\Sigma}$ of $\partial W=M$ , $\omega$ is exact.

Start by building J-holomorphic curves in the product part of the completion using a stable Hamiltonian structure that is nice with respect to the spinal open book decomposition of $M$ .

Since $\omega|_{M_{\Sigma}}$ is exact, if $\pi_P: M_P\to S^1$ is the paper fibration, $\omega$ is cohomologous to $d\pi_P\wedge \eta$ for a closed 1-form $\eta$ supported in $M_P$ .

On the spine, $M_{\Sigma}\cong S^1\times \Sigma$ and a compatible contact form is one whose Reeb vector field points in the $S^1$ direction. We can construct such a contact form as follows. Choose a complex structure $j$ on $\Sigma$ and a plurisubharmonic function $\phi: \Sigma \to \mathbb{R}$ which is constant on boundary components of $\Sigma$ , and setting $\sigma = -d\phi\circ j$ (such a plurisubharmonic function exists because $\Sigma$ has boundary). Then let $\alpha = d\theta+\sigma$ where $\theta$ is the $S^1$ coordinate on $M_{\Sigma}$ .

Proposition: Given the above assumptions, it is possible to deform $(W,\omega)$ near $\partial W$ such that there is a SHS on the boundary $(\lambda, \Omega)$ satisfying:
(1) In the spine away from the paper, $M_{\Sigma}$ , the stabilizing 1-form $\lambda = d\theta +\sigma$ and $\Omega=d\lambda$ .
(2) In the paper, $\pi_P: M_P\to S^1$ , the stabilizing 1-form $\lambda=d\pi_P$ and $\Omega = kd\alpha+d\pi_P\wedge \eta$ for some large $k$ where $\alpha$ is a “Giroux form” i.e. a contact form (or the cornered version) compatible with the spinal open book (so $d\alpha$ is positive on the pages).

Using this Stable Hamiltonian Structure to define the completion, there exists an almost complex structure $J$ satisfying:
(1) $\mathbb{R}$ -invariant on the $[0,\infty)\times M$ piece
(2) Each page $\times \{0\}$ is $J$ invariant
(3) For each gradient flowline $\gamma$ of the plurisubharmonic function $\phi:\Sigma \to \mathbb{R}$ which defined the Liouville 1-form $\sigma$ , there is a lift of $S^1\times \gamma\subset M_{\Sigma}$ in $[0,\infty)\times M$ to a $J$ -holomorphic half-cylinder $u_{\gamma}:[0,\infty)\times S^1\to [0,\infty)\times M$ .

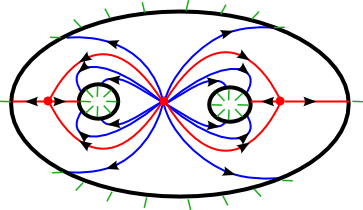
Here is a picture of some example gradient flowlines (in blue and red) on $\Sigma$ , which should exit the boundary of $\Sigma$ and land on a page (indicated by the green lines).

(4) Each page $\times \{0\}$ matches up to a union of the half cylinders $u_{\gamma}$ to form a finite energy embedded $J$ -holomorphic curve.

In fact there is a family of such $J$ -holomorphic curves, of index $2-2g(P)$ for a page $P$ . Therefore when we have at least one page of genus zero, there is a 2-dimensional family of $J$ -holomorphic curves which start filling up the completion $\widehat{W}$ . The space of points hit by such $J$ -holomorphic curves is open, and closed if you include all possible degenerations of the curves. The generic curves are genus zero (a genus zero page with some cylinders attached). These can degenerate in two ways:

Either the vanishing cycle splits the curve into different components each with some bounday or it bubbles off a closed sphere. It is possible to show that if it bubbles off a closed sphere, this sphere has self-intersection number -1 which implies $\widehat{W}$ is not minimal. So if we assume we have a minimal weak symplectic filling, the degenerations must split off pieces with boundary and these types of degenerations can only happen finitely many times (since there are finitely many boundary components). In the end, this implies that the space of points hit by these (possibly degenerate) J-holomorphic curves is both open and closed so (assuming our filling was connected) it is the whole of $\widehat{W}$ .

To get a Lefschetz fibration, one must restrict to a compact subdomain of the (noncompact) symplectic completion. This can be done in the case that the spinal open book decomposition is simple.

News from University of Minnesota 4-manifolds workshop

3 responses to “News from University of Minnesota 4-manifolds workshop”

Leave a comment Cancel reply

Recent Posts

Archives

Categories

Meta

News from University of Minnesota 4-manifolds workshop

Share this:

Related

3 responses to “News from University of Minnesota 4-manifolds workshop”

Leave a comment Cancel reply

Recent Posts

Archives

Categories

Meta